基礎統計学の勘どころ #4 回帰分析

前回↓

ryosuke-okubo.hatenablog.com

回帰分析
決定係数
補足

回帰分析

前置き

例は#3と同じものを用いる。

年齢	29	31	35	39	40	49	56	63
血圧	106	113	110	124	130	128	142	155

f:id:ryosuke_okubo:20190201160006p:plain

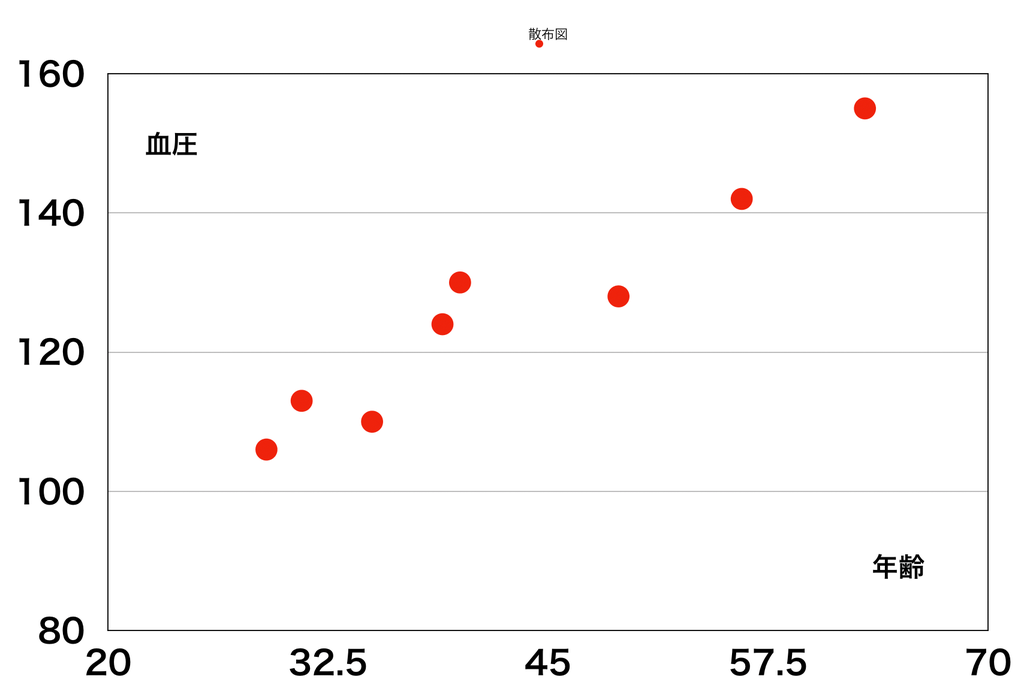
この散布図をみると，年齢と血圧の関係が $y=ax+b$ で近似できそうである。

f:id:ryosuke_okubo:20190209112129p:plain

こうすれば，今与えられていないデータに関しても年齢から血圧を予測することができるようになる。このように回帰分析とは，得られたデータを関数でモデル化することを目的とする。回帰分析では，おおよそ次のステップをふむ。

モデルの定義
残差の定義
残差の最小化

モデルの定義

一般に，真の単回帰直線は

$y_i = \beta_0 + \beta_1 x_i + \epsilon_i$

と表される。ここで， $x_i$ は独立変数， $y_i$ は従属変数， $\epsilon_i$ は誤差である。また $\beta_0,\beta_1$ を回帰係数といい，これを推定の対象とする。

誤差については，以下を仮定している。

平均は0
分散は一定値をとる
異なる誤差どうしは互いに無関係

誤差についてはあまり深く考えず，測定誤差のようなものと解しておけばよい（誤差は神のみぞ知る）。

では，与えられたxとyの値から回帰係数 $\beta_0,\beta_1$ を推定して，モデルを推定しよう。推定で得た単回帰直線を

$\hat{y_i} = \hat{\beta_0} + \hat{\beta_1} x_i$

と表すことにする。ここで $\hat{\beta_0},\hat{\beta_1}$ と $\beta_0,\beta_1$ は必ずしも一致するとは限らないことに注意。補足を参照。

残差の定義

さて，以下の直線のうちどれが近似できているものだろうか？

f:id:ryosuke_okubo:20190211183426p:plain

f:id:ryosuke_okubo:20190211183429p:plain

f:id:ryosuke_okubo:20190211183432p:plain

見たところ，左の方が良さそうである。では何が違うのか？

f:id:ryosuke_okubo:20190211183438p:plain

実測値である $y_i$ と推測値である $\hat{y_i}$ の差

$e_i=y_i-\hat{y_i}$

である残差が違っている。これが小さいほど，よい近似と言えそうである。

ちなみに誤差との違いとして，誤差は測定され得ないが，残差は測定可能であることがあげられる。したがって回帰係数 $\beta_0,\beta_1$ の推定には残差を用いることになる。

残差の最小化

ここで最小二乗法について説明しておく。

ある関数 $f(x)$ の最小値は，

$f'(x)=0$

となる $x$ から求められる。

f:id:ryosuke_okubo:20190211184442p:plain

$z=f(x,y)$ のような多変数関数で最小値を求めるには，偏微分を求めて

$\frac{\partial z}{\partial x} = 0,\frac{\partial z}{\partial y} = 0$

となるxとyの値を連立方程式で解く。

偏微分は従属変数が2つ以上ある関数において，1つの従属変数ごとで微分することと思えばよい。 $z=x^2+y^2$ を例にイメージしてみよう。

f:id:ryosuke_okubo:20190211185737p:plain

この関数は，いわばお椀みたいな形をとる。ここで，x軸とy軸のそれぞれに沿ってスライスしてみる。

f:id:ryosuke_okubo:20190211191141p:plain

すると， $y=x^2$ と同じ形となる。これは片方の変数を固定して定数とみなしたときの関数に相当する。これで1つずつ微分を求めていくと

$\frac{\partial z}{\partial x} = 2x = 0$ ， $\frac{\partial L}{\partial y} = 2y = 0$

より，

$x=0,y=0$ のとき，最小値 $z=0$

となる。

では回帰分析に適用してみる。回帰分析では残差の2乗和

$L(\hat{\beta_0},\hat{\beta_1}) = \sum_{i=1}^n e_i^2 = \sum(y_i-\hat{y_i})^2 \\ \displaystyle =\sum(y_i-\hat{\beta_0}-\hat{\beta_1 x_i})^2$

を最小にする $\hat{\beta_0},\hat{\beta_1}$ を求めていく。このために， $L$ を $\hat{\beta_0}$ と $\hat{\beta_1}$ で偏微分して，

$\frac{\partial L}{\partial \beta_0} = 0$ ， $\frac{\partial L}{\partial \beta_1} = 0$

とすると，式変形により次の正規方程式を得る。

$\Biggl\{\begin{eqnarray} n\hat{\beta_0}+(\sum x_i)\hat{\beta_1} = \sum y_i \\ (\sum x_i)\hat{\beta_0}+(\sum x_i^2)\hat{\beta_1} = \sum x_i y_i \end{eqnarray}$

この正規方程式を解くことで，残差の2乗和を最小にする $\hat{\beta_0}$ と $\hat{\beta_1}$ が求められる。整理すると，

$\hat{\beta_0} = \bar{y} -\hat{\beta_1}\bar{x}$ ， $\hat{\beta_1} = \frac{s_{xy}}{s_x^2}$

となる。

たとえば年齢と血圧についての単回帰直線は

$\bar{x} = 42.75$ ， $\bar{y} = 126$ ， $s_x^2 = 129.$ ， $s_{xy} = 170$ より

$\hat{\beta_1} = \frac{170}{129.}=1.32$

$\hat{\beta_0} = 126 -1.32 \times 42.75 = 69.57$

→ $y=1.32x+69.57$

と表せる。

最小二乗法の一般的な解法は，たとえば以下に詳しい。

最小二乗法の行列表現（一変数，多変数，多項式） | 高校数学の美しい物語

決定係数

推定された回帰直線がデータとの当てはまりがよいか確認するために，決定係数 $R^2$ を求める。そのために，実際のデータと推定された回帰直線から「全変動」「回帰変動」「残差変動」の3つを見ていく。

全変動：データ全体のばらつき， $\sum(y_i-\bar{y})^2$
回帰変動：回帰直線によるばらつき， $\sum(\hat{y_i}-\bar{y})^2$
残差変動：回帰直線とデータのずれ， $\sum(y_i-\hat{y_i})^2$

これらを用いて，決定係数 $R^2$ は次のように定義される。

$R^2=\frac{\sum(\hat{y_i}-\bar{y})^2}{\sum(y_i-\bar{y})^2}$ ， $0 \le R^2 \le 1$

要するに決定係数とは，データ全体のばらつきのうち回帰直線によるばらつきがどれだけ影響しているかを示している。つまり $R^2$ が1に近いほど当てはまりがよい。

なお，決定係数は相関係数の2乗と等しい関係にある。

$R^2 = r_{xy}^2$

したがって，「相関関係が強い↔︎回帰直線の当てはまりがよい」ということがいえる。

決定係数の導出過程については以下に詳しく書いてある。

http://www.geisya.or.jp/~mwm48961/statistics/coef_det1.htm

補足

単回帰直線に「真の」とか「推測で得た」とあるが，一体何が違うのか？と思われるだろう。これは推測統計学における「母集団」と「標本集団」の違いととらえていただければと思う。今回の例では与えられたデータの特徴をつかむことに重点をおいたが，回帰分析では「与えられたデータから未知のデータを予測する」こともできる。詳しいことについては後日書く予定である。

次回↓

ryosuke-okubo.hatenablog.com