基礎統計学の勘どころ #6 代表的な確率分布
前回↓
確率分布の代表例として,離散確率分布から2項分布とポアソン分布,連続確率分布から正規分布と標準正規分布は最低限知っておくべきである。本記事ではそれらの性質について説明する。
2項分布とポアソン分布
2項分布
「コインを投げて表が出るか裏が出るか」のように,何かを行ったときに起こる結果が「成功」か「失敗」かの2つしかない試行のことをベルヌーイ試行という。このとき表が出る(成功)確率をとすると,裏が出る(失敗)確率は
である。
この試行をn回行って成功する回数Xがしたがう確率分布が2項分布であり,成功する確率をpとすると,
と表記される。
この試行をn回行ってk回成功する確率は次式で表される。
式の意味を,具体例で説明してみる。
例:サイコロを3回投げて,1の目がk回出るときの確率変数X
この試行はであり,k回成功する確率は
式の意味:
の部分はk回成功する組み合わせの個数について示している。
また,はある1つの組み合わせについて,k回成功してn-k回失敗する確率を示している。
表にまとめる。
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 組み合わせの個数 | ||||
| ある1つの組み合わせについて,k回成功してn-k回失敗する確率 | ||||
| k回成功する確率 |
グラフ

において,期待値と分散は以下のようになる。
,
(証明略,はじめのうちは暗記でもよい)
例において,なので
,
2項分布の詳細,証明:
二項分布の平均と分散の二通りの証明 | 高校数学の美しい物語
ポアソン分布
ベルヌーイ試行において,nが十分大きくpが非常に低い場合,とおいて,Xはポアソン分布にしたがうと考えられる(
)。これは交通事故の回数などに,よく当てはまるとされている。
ポアソン分布にしたがう確率変数は,期待値と分散が等しいという特徴がある。
2項分布からポアソン分布を導出する過程については,ポアソンの極限定理を調べてほしい。
例:
なお,その他の離散確率分布については,以下の記事でざっくりと解説している。
正規分布と標準正規分布
正規分布
自然現象の多くは正規分布にしたがうと考えられており,そのため正規分布は確率分布の中でも特別視されている。正規分布は確率変数の平均
と分散
により規定され,
と表記される。確率密度関数
は
である。また確率変数の期待値と分散は次のとおりである。
,
グラフ(,
)

正規分布が持つ性質について,以下のことは重要である。いずれも後の計算問題で多用される。
- 確率密度は0から1の値をとる(負の値をとらない)。
- 確率密度の合計は1
を軸に左右対称のグラフを描く
の範囲内に,全体の約95%が含まれる(重要)
ここで,2項分布と正規分布の関係について触れておく。離散確率分布である2項分布は,
が十分大きいとき,連続確率分布である正規分布
に近似できる。
例:サイコロを3回投げて,1の目がk回出るときの確率変数X
をもし正規分布で近似すると,より
となる。
標準正規分布
確率変数が
にしたがうとき,
(
から
への標準化)
とした新たな確率変数は
にしたがう。この確率分布を標準正規分布という。
標準化の過程を以下に図示する。
-
確率変数
から平均
を引く。
→平均が0に変換される。

黒:もとの確率分布 赤:平均 を引いたもの
-
標準偏差
で割る。
→ 標準偏差,分散が共に1に変換される。

黒:平均 を引いたもの 赤:さらに標準偏差
で割ったもの(標準正規分布)
標準化をすることで,いかなる正規分布も標準正規分布として扱えるようになる。これにより確率の計算が容易になる。
計算問題の例
偏差値を例に,正規分布の計算問題を解いてみる。偏差値とは点数の分布を,平均,分散
の正規分布(
)に変換した指標である。
例題:試験の点数を偏差値に変換したとき,以下の値を求めよ。
(1) 65以下の者が占める割合
(2) 全体の95%が含まれる偏差値の範囲(平均を軸に左右対称とする)
解き方としては,まずは分布の標準化を行う。こうすることで後の計算が楽になる。そのあとについては
方法がある。ここでは2. について説明する。なお標準正規分布表にはいろいろ種類があるが,本記事では統計検定の付表にある資料に基づいて説明する。
(1)
グラフ

手順
-
まずは確率変数の標準化を行う。偏差値にしたがう確率変数を
とすると,求める値は
と表せる。標準化の式は,
なので,
は
に変換される。

標準化した後のグラフ,軸の目盛に注目 -
標準正規分布表では片側の確率しか求められないため,左右に分割する。

-
左側の確率(~0)を求める。ここで
- 確率密度の合計は1
を軸に左右対称のグラフを描く
であることから,左側の確率の確率は0.5と決まる
-
右側の確率(0~1.5)を求める。標準正規分布表をみると,
であることがわかる。
*標準正規分布表の読み方

縦軸は小数点第2位まで,横軸は小数点第3位を示す ここで右側全体の確率は0.5なので,求める確率は0.5-0.0668=0.432と決まる。
-
左側と右側を足して,0.5+0.432=0.932,つまり約93.2%が含まれる。
(2)
問題について数式で表すと,となる
を求めることになる。ここで,
の範囲内に,全体の約95%が含まれる
より,である。あとは値を代入して,
より
つまり全体に対して,偏差値30~70の間に約95%が含まれていることになる。

ところで,
の範囲内に,全体の95%が含まれる
ことがなぜ言えるのだろうか?ここで標準正規分布表を用いて示してみる。
標準正規分布表をみると,
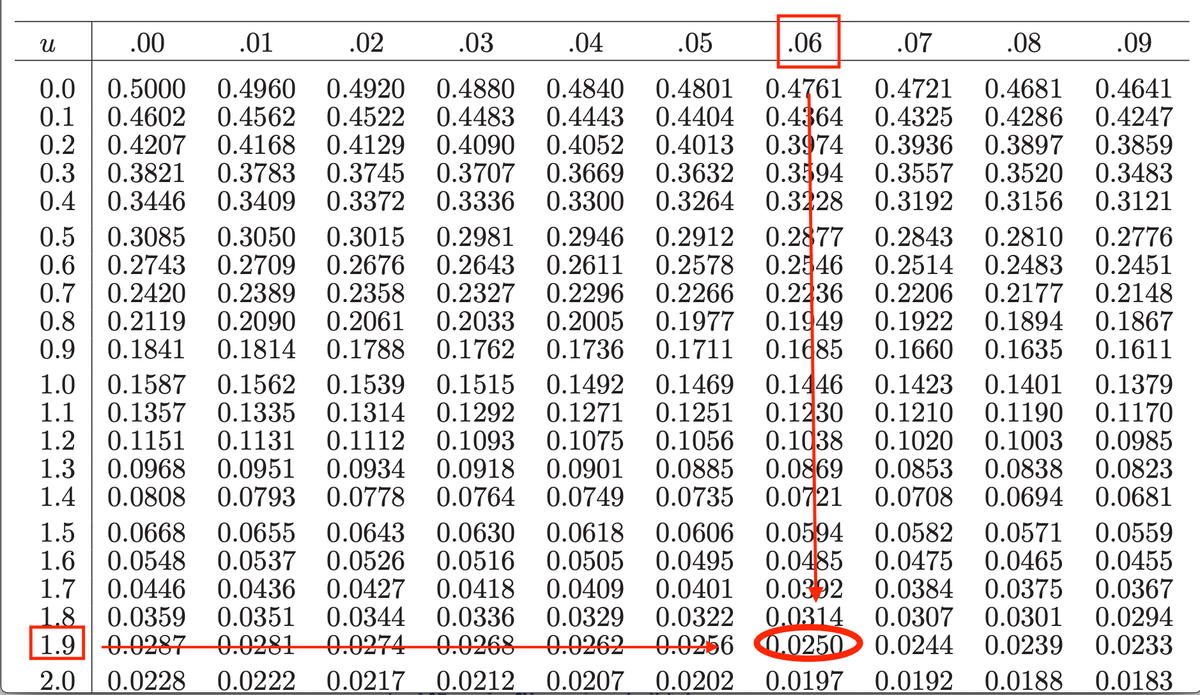
であることがわかる。また,左右対称であるためである。このことから,
となる。ここで標準化の式よりZからXに変換して,
これで,
の範囲内に,全体の95%が含まれる
ことが示された。この文,あえて何回も繰り返して書いたが,後々区間推定や検定をする際に重要な概念なので,覚えておいてほしい。
正規分布のより詳しい内容は,以下の記事にまとめてある。
次回↓