十の並列した脳

何でも勉強する，毎週月木曜に投稿予定

「Pythonによるベイズ統計モデリング」まとめ #1

統計学 ベイズ統計


「Pythonによるベイズ統計モデリング―PyMCでのデータ分析実践ガイド― 」：

 

Pythonによるベイズ統計モデリング: PyMCでのデータ分析実践ガイド

Pythonによるベイズ統計モデリング: PyMCでのデータ分析実践ガイド

 

 

まえがきによると，「文系向け」「実践志向」「Python/PyMC3」を特徴としている。読んだところ，それに偽りはなく手を動かすことでなんとなくからでも理解が進む構成になっている。本記事では，この本の概要について5回に分けて掲載する。#1では第1章について扱う。

 

 

全体の概要 

目次

第1章　確率的に考える－ベイジアン推論入門
第2章　確率プログラミング－PyMC3入門
第3章　複数パラメータの取り扱いと階層モデル
第4章　線形回帰モデルによるデータの理解と予測
第5章　ロジスティック回帰による結果変数の分類
第6章　モデル比較
第7章　混合モデル
第8章　ガウス過程

 

第1章　確率的に考える－ベイジアン推論入門

ベイズの定理

まずは理論の話である。「あらかじめ知っている情報に，得られたデータをかけると，情報が更新される」ことを数式で表している。

 

{\displaystyle p(H|D) = \frac{p(D|H)p(H)}{p(D)}}

この式がベイズの定理であり，乗法定理を変形して容易に得られる。Hを仮説，Dをデータと読み替えると，各パラメータは次のように示される。

  • p(H)：事前分布，データを知る前にパラメータについて知っていること
  • p(D|H)：尤度，与えられたパラメータのもっともさ
  • p(H|D)：事後分布，ベイジアン分析の結果
  • p(D)：エビデンス，規格化定数として扱う

p(D)は比例定数として扱えるので，実質次の式が重要である。

{\displaystyle p(H|D) \propto p(D|H)p(H)}

 

コイン投げ問題の例

[1]　一般モデルの推定

まず偏りの概念を一般化する。

  • 偏りが0→裏しか出ない
  • 偏りが1→表しか出ない
  • 偏りが0.5→表と裏が半々出る

偏りのパラメータを \theta，N回投げて表が出た回数をyとすると，次の式で表される。

{\displaystyle p(\theta|y) \propto p(y|\theta)p(\theta)}

 

[2]　尤度の選択

コイン投げの試行において，尤度は2項分布となる。

{\displaystyle p(y|\theta) = \binom{N}{y}\theta^{y} (1-\theta)^{N-y}}

 

[3]　事前分布の選択

ベータ分布を用いる。

{\displaystyle p(\theta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}\theta^{\alpha} (1-\theta)^{\beta-1}}

ベータ分布を使う理由として，

  • 0と1の区間に制限されている
  • パラメータによって様々な形をとる
  • 2項分布の共役事前分布である

ことがあげられる。

 

[4]　事後分布の計算

ベイズの定理より，

{\displaystyle p(\theta|y) \propto\binom{N}{y}\theta^{y} (1-\theta)^{N-y}\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}\theta^{\alpha} (1-\theta)^{\beta-1}}

\thetaに依存する項のみで簡略化すると，

{\displaystyle p(\theta|y) \propto\theta^{\alpha-1+y} (1-\theta)^{\beta-1+N-y}}

つまり，次のベータ分布で表される。

{\displaystyle p(\theta|y) = Beta(\alpha_{prior}+y,\beta_{prior}+N-y)}

 

[5]　例題

(1)　5回投げて2回表が出た，事前分布は {\displaystyle Beta(1,1)}とする

(2)　さらに5回投げて1回表が出た，事前分布は(1)の確率分布とする

 

(1)　 {\displaystyle Beta(1,1)}は一様分布と等価であり，何も知らないことを表す。

[4]の式に各パラメータを代入することで事後分布が得られる。

{\displaystyle p(\theta|y) = Beta(1+2,1+3) = Beta(3,4)}

事後分布のピークは \theta = 0.4周辺にある。

 

(2)　事前分布が {\displaystyle Beta(3,4)}であるので，

{\displaystyle p(\theta|y) = Beta(3+1,4+4) = Beta(4,8)}

事後分布のピークは \theta = 0.3周辺にある。

f:id:ryosuke_okubo:20190131202446p:plain
f:id:ryosuke_okubo:20190131202451p:plain

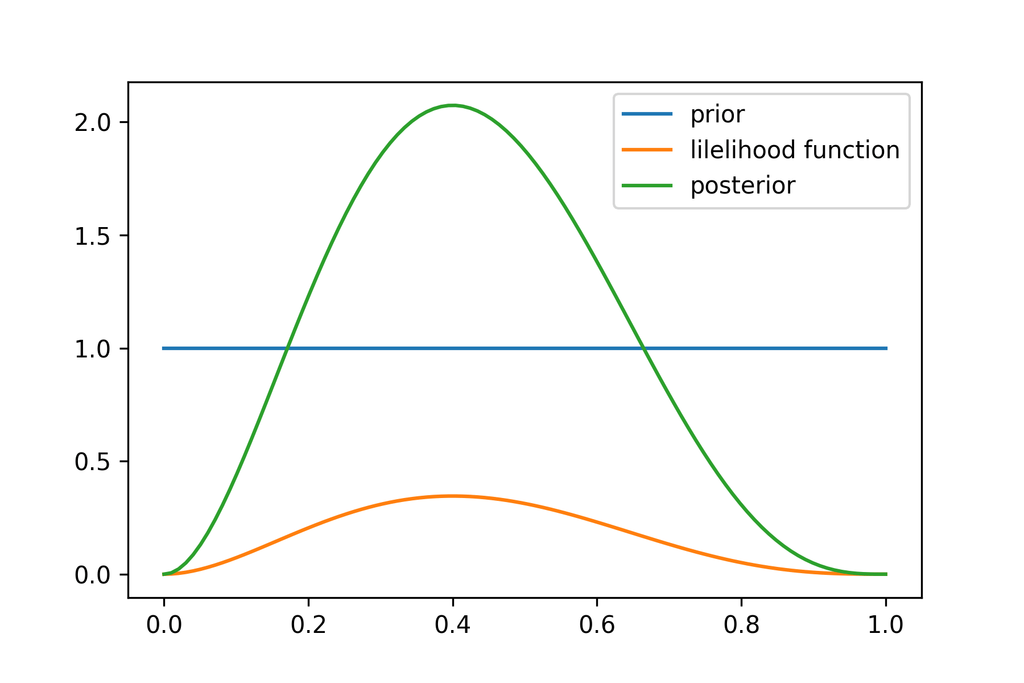
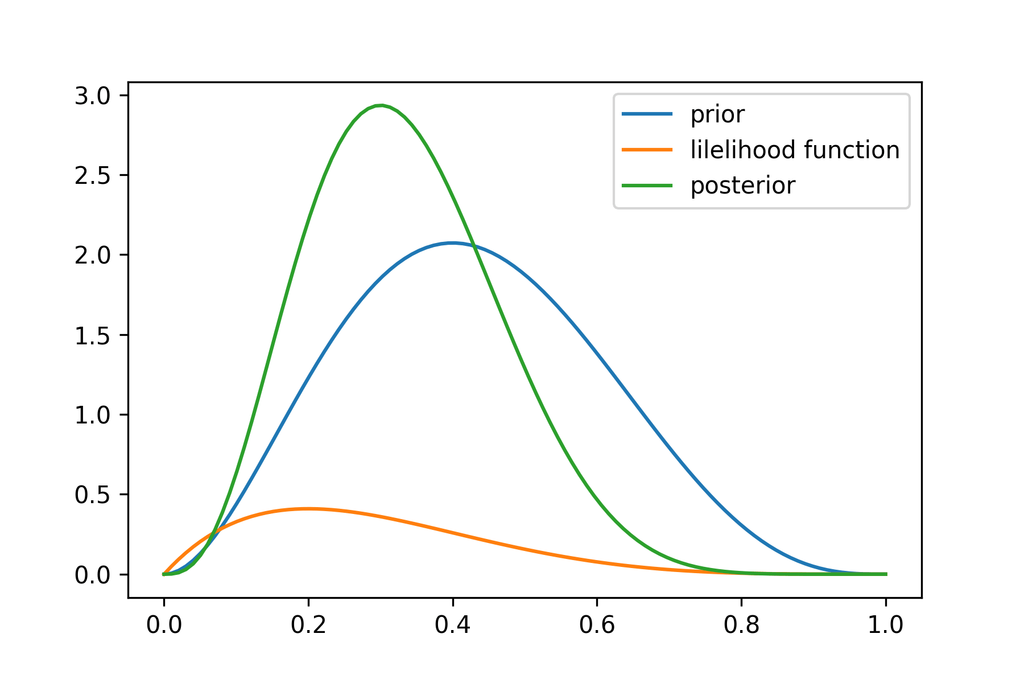
作図にあたっては次の記事を参考にした。

二項分布のパラメータ（ベータ分布）の事後分布を尤度関数で求める - Qiita

 

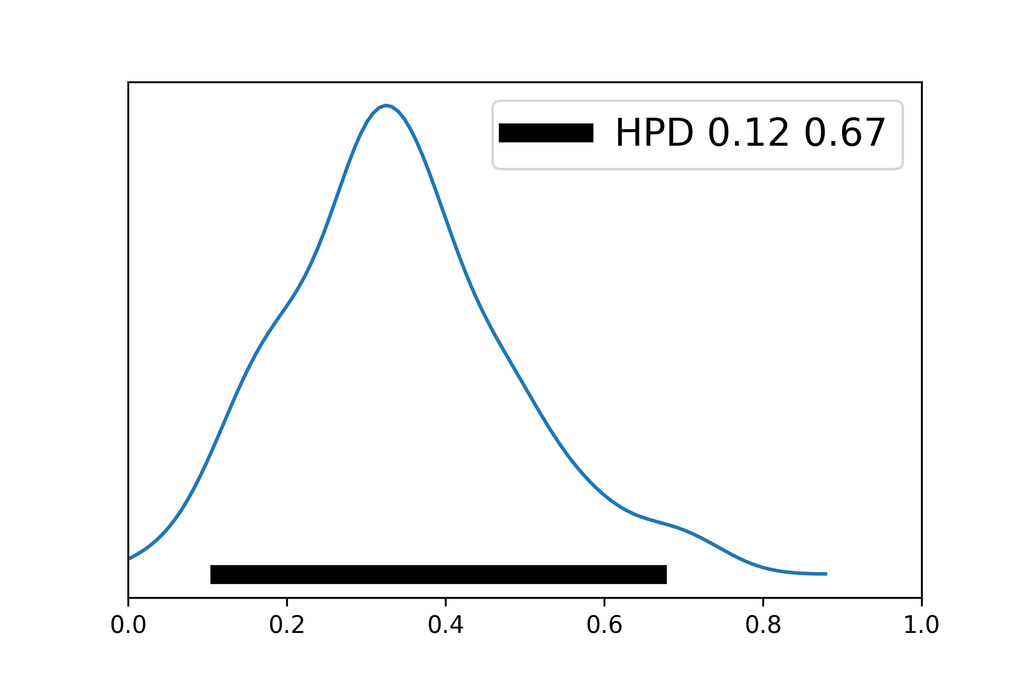
[6]　事後分布の要約

最高事後密度（HPD）が汎用される。例題についての95%HPDを示す。

f:id:ryosuke_okubo:20190201165346p:plain
f:id:ryosuke_okubo:20190201165349p:plain

 

次回↓

 

ryosuke-okubo.hatenablog.com