確率・統計の勉強 #8 ガンマ分布からカイ二乗分布へ，統計検定1級問題をのぞいてみる

藤田岳彦「弱点克服大学生の確率・統計」：

弱点克服大学生の確率・統計

作者: 藤田岳彦
出版社/メーカー: 東京図書
発売日: 2010/04/09
メディア: 単行本
購入: 6人クリック: 9回
この商品を含むブログを見る

前回↓

ryosuke-okubo.hatenablog.com

問題
解法
- ガンマ分布
ベータ分布
カイ二乗分布

問題

統計検定1級統計数理（2018年11月）問1[2]より改変

自由度 $n-1$ のカイ二乗分布にしたがう確率変数 $Y$ について， $E(Y)$ と $V(Y)$ を求めよ。

実際の問題では確率変数 $Y$ の確率密度関数が与えられ，これの期待値と分散をガンマ関数の形に変形して求められる。ガンマ関数については#6で解説した。

ryosuke-okubo.hatenablog.com

本記事では，カイ二乗分布がガンマ分布から構成されるところから説明する。関連して，ベータ分布についても触れておく。

解法

ガンマ分布

基本事項

表記：

$X \sim \Gamma(a,\lambda)$

確率密度関数：

$f(x) = \frac{\lambda^a}{\Gamma(a)} x^{a-1} e^{-\lambda x} \ (x \gt 0 ,a \gt 0,\lambda \gt 0)$

期待値と分散：

$E(X) = \frac{a}{\lambda}, V(X) = \frac{a}{\lambda^2}$

グラフ

f:id:ryosuke_okubo:20190227175147p:plain

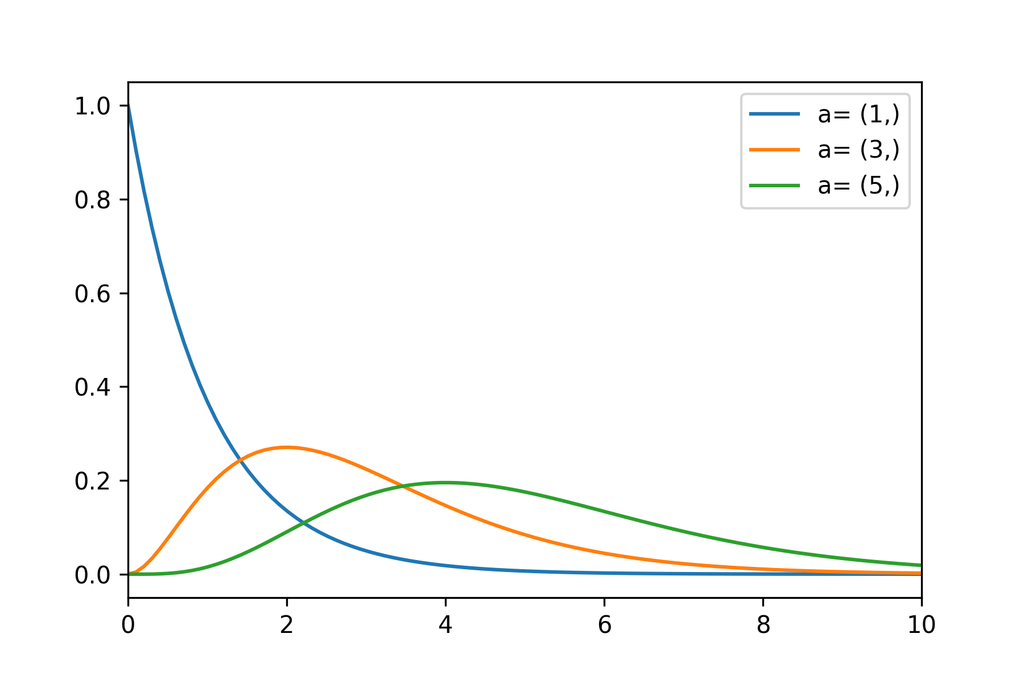
ガンマ分布は連続確率分布の一種であり，部品の寿命や待ち時間などに当てはまる。分布の形はパラメータ $a$ と $\lambda$ により決定される。正規化にはガンマ関数が用いられている。

ここで正規化項の導出について説明しておく。ガンマ関数への変換が重要である。

$1 = c \int_0^{\infty} x^{a-1} e^{-\lambda x} dx$

ここでガンマ関数の形を作るために変数変換 $u = \lambda x$ を施すと，

$= c \int_0^{\infty} (\frac{u}{\lambda})^{a-1} e^{-u} \frac{1}{\lambda}du \\ \displaystyle = c \frac{1}{\lambda^a}\int_0^{\infty} u^{a-1} e^{-u} du$

積分をガンマ関数に変換して，

$= c \frac{1}{\lambda^a}\Gamma(a)$

よって，

$c = \frac{\lambda^a}{\Gamma(a)}$

期待値と分散も同様にして導出できる（各自解いてみてほしい）。

他の確率分布との関係

以下に列挙する。

指数分布 $Exp(\lambda)$ ： $a=1$ の場合（ $\Gamma(1,\lambda)$ ）に該当する。
標準正規分布の2乗 $N(0,1)^2$ ： $\Gamma(\frac{1}{2},\frac{1}{2})$ に該当する。

導出→ $N(0,1)^2$ の分布関数について，

$F_{N(0,1)^2} (x) = P(N(0,1)^2 \leq x) =P(\sqrt{-x} \leq N(0,1) \leq \sqrt{x}) \\ \displaystyle = \Phi(\sqrt{x}) - \Phi(\sqrt{-x})$

ここで $\Phi(x) = \int_{-\infty}^x \frac{1}{\sqrt {2 \pi}} e^{-\frac{x^2}{2}} dx$ （標準正規分布の分布関数）

両辺を微分して確率密度関数とする，

$f_{N(0,1)^2} (x) = \frac{d}{dx}(\Phi(\sqrt{x}) - \Phi(\sqrt{-x})) \\ \displaystyle = \frac{1}{\sqrt {2 \pi}} x^{-\frac{1}{2}}e^{-\frac{1}{2}x} = f_{\Gamma(\frac{1}{2},\frac{1}{2})}$

再生性

$X \sim \Gamma(a,\lambda), Y \sim \Gamma(b,\lambda)$ で独立のとき， $X+Y \sim \Gamma(a+b,\lambda)$ が成り立つ。これをガンマ分布の再生性という。確認するには確率密度関数への代入で十分だが，証明にはモーメント母関数を用いる必要がある（ここでは省略）。

ベータ分布

似たような分布として，ベータ分布も重要である。

表記：

$X \sim \beta(a,b)$

確率密度関数：

$f(x) = \frac{1}{B(a,b)} x^{a-1} (1-x)^{b-1} \ (x \gt 0 ,a \gt 0,b \gt 0)$

期待値と分散：

$E(X) = \frac{a}{a+b}, V(X) = \frac{a(a+1)(a+2)}{(a+b)^2 (a+b+1)}$

グラフ

f:id:ryosuke_okubo:20190227175210p:plain

f:id:ryosuke_okubo:20190227175214p:plain

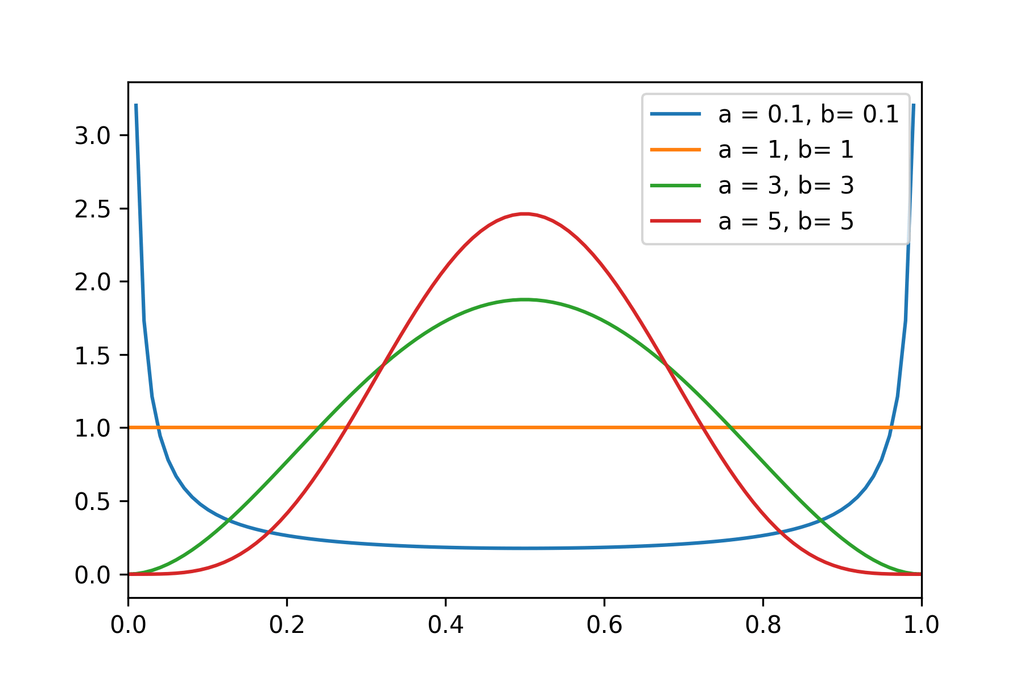
カイ二乗分布

独立に標準正規分布にしたがう確率変数 $X_1,X_2,...,X_n$ をとる（ $X_1 \sim X_2 \sim ... \sim X_n \sim N(0,1)$ ）。このとき，

$Y_n = \sum_{i=1}^n X_i^2$

のしたがう分布を「自由度 $n$ のカイ二乗分布」といい， $\chi_n^2$ で表す。カイ二乗分布は推計統計学における適合度検定などで用いられる。

グラフ

f:id:ryosuke_okubo:20190227175317p:plain

自由度 $n=1$ のカイ二乗分布について，分布は $X_i^2 \sim N(0,1)^2$ なので， ${\displaystyle\chi_1^2 \sim \Gamma(\frac{1}{2},\frac{1}{2})}$ である。さらにガンマ分布の再生性より， ${\displaystyle\chi_n^2 \sim \Gamma(\frac{n}{2},\frac{1}{2})}$ である。