基礎統計学の勘どころ #3 散布図と相関分析

前回↓

次のデータは，8人の健康な女性の血圧値（収縮期血圧）である。

106 113 110 124 130 128 142 155

統計量を計算してみると，平均値：126，標準偏差：15.60となる。

ところで，このばらつきには何か原因があるのだろうか。例えば年齢との関係を調べてみると，次のようにまとめられた。

年齢	29	31	35	39	40	49	56	63
血圧	106	113	110	124	130	128	142	155

年齢の高さと血圧の高さには関係がありそうである。この関係を図で表しすために「散布図」を用いてみる。散布図は2つの変数の量をプロットしたものである。

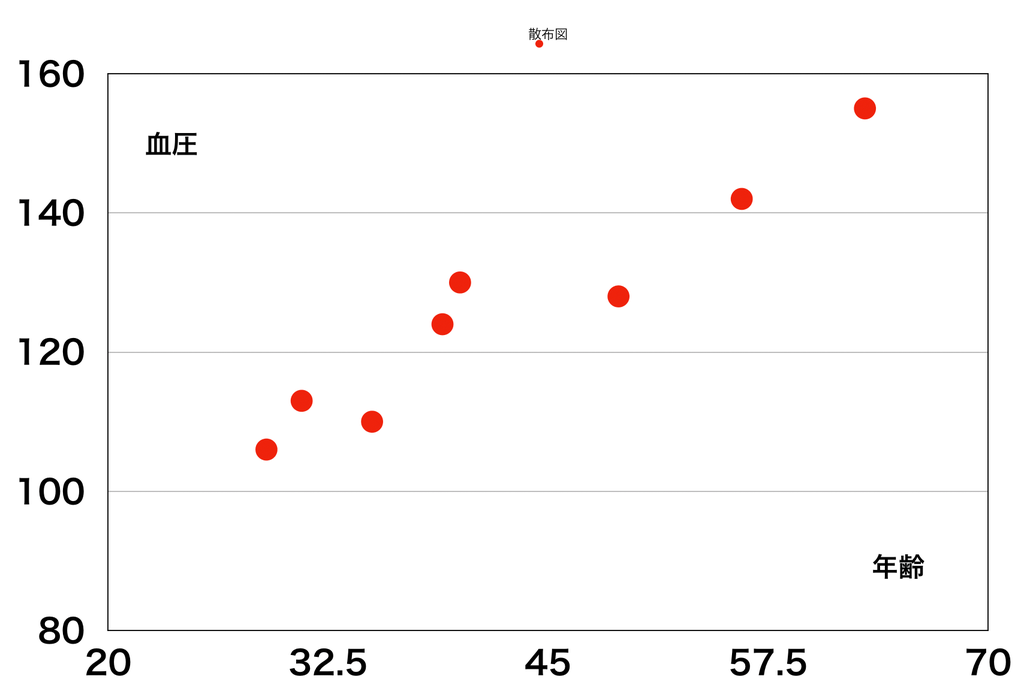
血圧の高さと年齢の高さには強い関係があることが，散布図から一目でわかる。

相関には「正負」と「強弱」があり，散布図から読み取れる。

今回の例では強い正の相関が見られる。

相関関係を1つの数字で表したのが，相関係数である。以下，その導出手順を示す。

手順

各変量の平均値 $\bar{x} \ , \bar{y}$ ，偏差 $x_i-\bar{x} \ , y_i-\bar{y}$ ，標準偏差 $s_x \ , s_y$ を求める。
共分散 $s_{xy}$ を求める。

$s_{xy} = \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})$

この式の意味について説明する。

図4 $(x_i-\bar{x})$ と $(y_i-\bar{y})$

散布図をそれぞれの平均を境に4つに分けると， $(x_i-\bar{x})$ の正負と $(y_i-\bar{y})$ の正負で分けられる。

図5 $(x_i-\bar{x})$ の正負と $(y_i-\bar{y})$ の正負による， $(x_i-\bar{x})(y_i-\bar{y})$ の正負

それで式中の $(x_i-\bar{x})(y_i-\bar{y})$ の正負についてみていくと，図6のように表せられる。散布図において右上と左下が正，左上と右下が負となる。

図6 共分散の正負

あとは正の区間に多いか，負の区間に多いかで，共分散の正負が決まってくる。実質，相関の正負が共分散によって決められているといえる。
相関係数 $r_{xy}$ を求める。

${\displaystyle r_{xy} = \frac{s_{xy}}{s_x s_y}}, \ -1\le r_{xy} \le 1$

相関係数は，共分散を-1から1の値に正規化したものである。相関係数については次のことが重要である。
- $r_{xy}$ が+1に近いほど，正の相関が強い
- $r_{xy}$ が-1に近いほど，負の相関が強い
- $r_{xy}$ が0に近いほど，相関が弱い

では，血圧の例について相関係数を求める。以下のような表を作成すると便利である。

	$x_i$	$y_i$	$x_i - \bar{x}$	$(x_i - \bar{x})^2$	$y_i - \bar{y}$	$(y_i - \bar{y})^2$	$(x_i - \bar{x})(y_i - \bar{y})$
	29	106	-13.75	189.	-20	400	(-13.75) × (-20)
	31	113	-11.75	138.	-13	169	(-11.75) × (-13)

	63	155	20.25	410.	29	841	20.25 × 29
$\sum$	342	1008	0	1033.5	0	1946	1360
$\frac{1}{n}\sum$	42.75 = $\bar{x}$	126= $\bar{y}$		129.= $s_x^2$		243.= $s_y^2$	170= $s_{xy}$
$\sqrt{}$				11.37= $s_x$		15.60= $s_y$