十の並列した脳

何でも勉強する，毎週月木曜に投稿予定

基礎統計学の勘どころ #7 推測統計学の考え方，点推定

統計学

前回↓

 

ryosuke-okubo.hatenablog.com

 

ここから3記事かけて，降圧薬（血圧を下げる作用をもつ）の臨床試験を例に，推測統計学について説明していく。

 

問題

新薬Aの血圧低下作用を知るために，患者20人を無作為に2群に分け，10人には新薬Aを，もう10人にはプラセボを投与する。何週間か投与して，最低血圧を測定すると以下の値となった。

投与                     平均 分散
新薬A 98.0 98.5 100.2 103.0 98.5 107.8 80.2 81.5 90.6 91.2 94.95 80.38
プラセボ 105.2 91.8 102.9 108.5 113.2 91.5 92.6 95.9 103.4 104.6 100.96 57.39

 

新薬Aとプラセボの平均には6くらいの差がある。この結果から，薬剤Aは血圧低下作用がある，と結論づけてもいいのだろうか？

 

この問題に対して，例えば以下のような疑問が予想される。

  • どれくらいが「差がある」と言えるのか？
  • 分散は気にしなくてよいのか？
  • たった20人での試験を，現実に適用できるか？

これらを考えるための基礎を，以下解説していく。 

 

 

推測統計学の背景

血圧が下がるかどうかが知りたいなら，該当する全世界の患者に投与すればわかることである。しかし実際には危なっかしくてできそうにない。そこで，何人かの患者にのみ投与して，その測定値をみて全世界の患者に作用が期待できるかを推測する。これが推測統計学の考え方である。

f:id:ryosuke_okubo:20190504103711p:plain

実際に分析の対象とする集団のことを母集団という（例では全世界の患者）。一方で，母集団から無作為に抽出された集団を標本という（例では選ばれた何人か）。母集団と標本にはそれぞれパラメータがあり，標本パラメータから母集団パラメータを推測するという手順を踏む。

標本の大きさとは，母集団から抽出した要素の個数をさす。

母集団には「有限母集団」と「無限母集団」がある。今回の例は有限母集団に当てはまる。無限母集団の例に，コイン投げで得られるデータがあり，投げた回数が標本の大きさに該当する。

 

ここで標本の抽出は無作為であることが重要である。血圧が下がった人だけを抽出して効果があることを証明する，というやり方をしてはいけない。

 

大数の法則と中心極限定理

推測統計学におけるエビデンスの保証は，大数の法則と中心極限定理の理論によるところが大きい。

 

大数の法則

大きさがNの母平均\muは

{\displaystyle \mu=\frac{1}{N}\sum_{i=1}^n x_i}

である。一方，大きさがnの標本平均\bar{x}は

{\displaystyle \bar{x}=\frac{1}{n}\sum_{i=1}^n x_i}

である。大数の法則は以下のように定義される。

定義（弱定理）：

{\displaystyle \lim_{n \to \infty} P(|\bar{x} - \mu | \gt \epsilon) = 0 \ (\forall \epsilon \gt 0)}

定義がどうのこうのについてはこれ以上触れない。その代わり，ざっくりとしたイメージはおさえておきたい。

意訳：

標本の大きさnが大きいほど，標本平均は母平均に近くなる

f:id:ryosuke_okubo:20190503115100p:plain

 

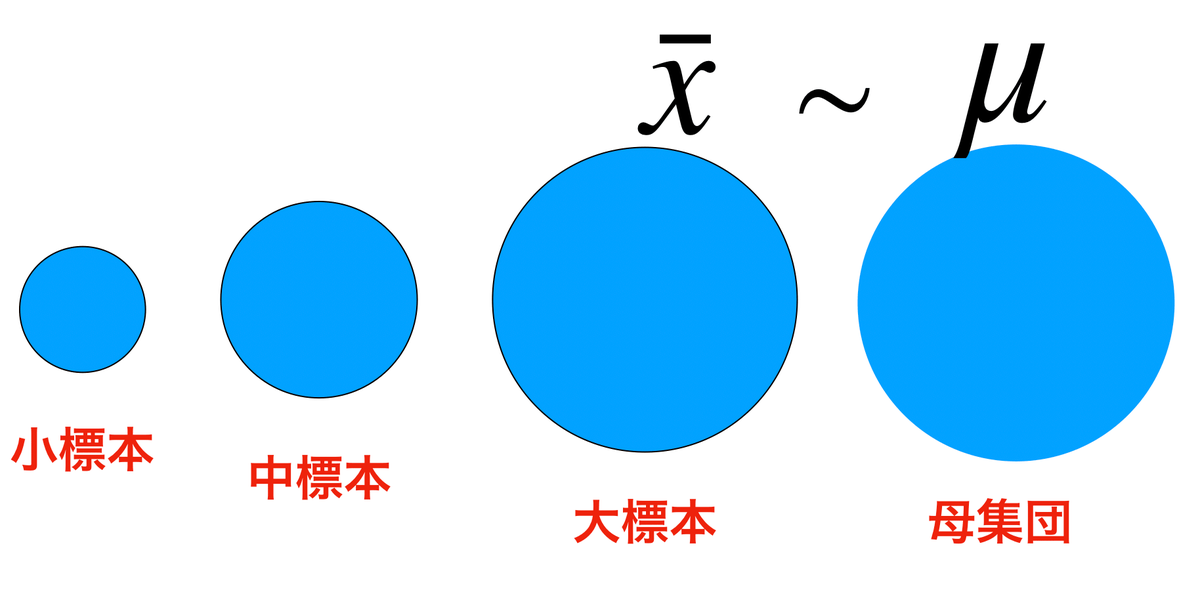
中心極限定理

母集団から標本を抽出して標本平均を求める，という動作を何回か繰り返す。そして得られた標本平均を分布で表す。

f:id:ryosuke_okubo:20190503115128p:plain

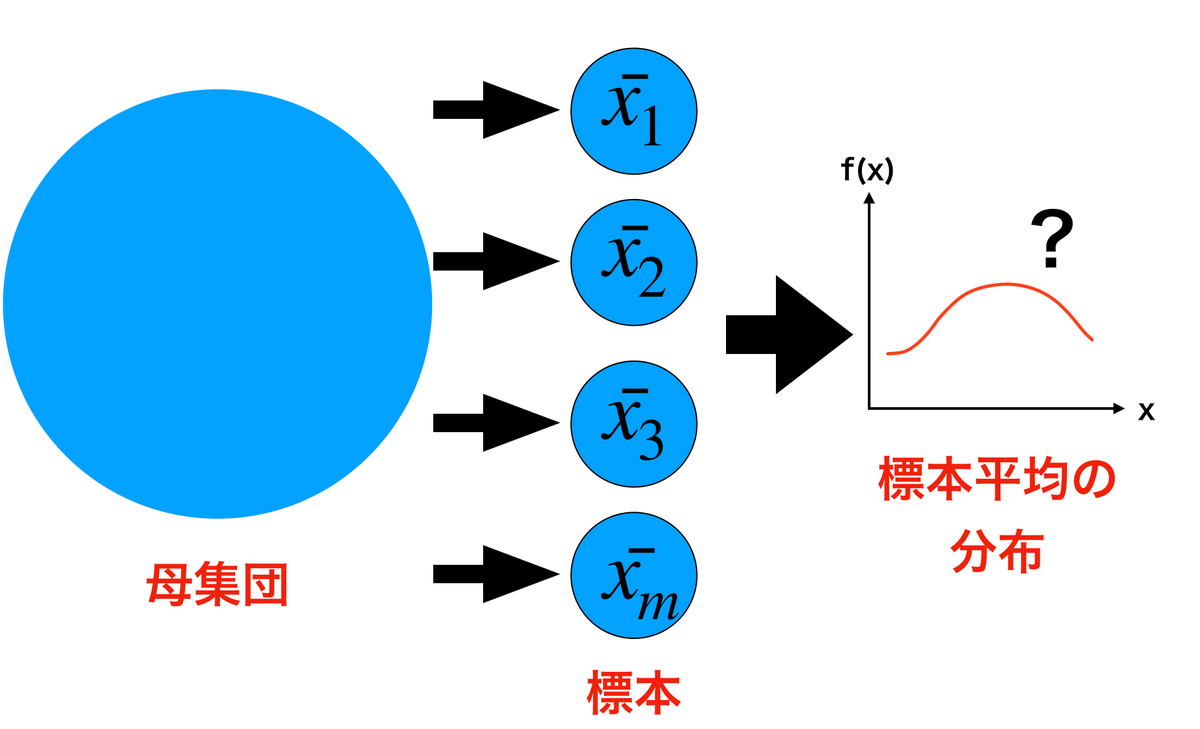
それぞれの標本平均は異なる値をとるだろうが，ある程度母平均に近いところに集中するだろう。これを具体的に示したのが中心極限定理である。

定義：

{\displaystyle \bar{x} \to N(\mu,\sqrt{\frac{\sigma^2}{n}})\ (n \to \infty)}

意訳：

標本の大きさnが大きいほど，標本平均の分布は正規分布{\displaystyle N(\mu,\sqrt{\frac{\sigma^2}{n}})}に近くなる

 

また，標本平均\bar{x}を標準化した

{\displaystyle z = \frac{\bar{x}-\mu}{\frac{\sigma^2}{n}}}

の分布は，標本の大きさnが大きいほど標準正規分布{\displaystyle N(0,1)}に近くなる。

ポイントとして，標本の大きさnが大きいほど分散に相当する{\displaystyle \sqrt{\frac{\sigma^2}{n}}}（標準誤差というパラメータ）が小さくなることは重要である。

 

点推定

概要

点推定は，標本パラメータを母集団パラメータにそのまま適用する推定である。 そんなことしていいのか，と思うかもしれないが，標本パラメータが以下の条件を満たせばOKである。

  • 不偏性：標本パラメータの期待値が，母集団パラメータに等しい
  • 一致性：標本の大きさを大きくすると，標本パラメータが母集団パラメータに近く

 

標本平均は条件を満たすので，そのまま採用される。

標本分散は，条件を満たさない。不偏性が満たされないのである（実際に期待値を求めてみるとわかる，ここでは省略）。 代わりに，推測統計では不偏標本分散

{\displaystyle s^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})^2}

を用いる。nではなくn-1で割るのがポイントである。

 

問題を解いてみる

表にある平均は「標本平均」であり，分散は「不偏分散」とする。

これより，新薬Aの母平均は94.95，母分散は80.38と点推定される。プラセボについても同様。

 

なんだそれだけか，と思うかもしれない。点推定においては本当にそれだけなのである。ただし，そこに推測統計学ならではの文脈が隠されていることを理解してほしい。

 

次回↓

 

ryosuke-okubo.hatenablog.com