十の並列した脳

何でも勉強する，毎週月木曜に投稿予定

確率・統計の勉強 #12（最終回） 最尤推定からクラメール・ラオの不等式まで

統計学 問題演習を通して理解する基礎統計勉強会まとめ

藤田 岳彦「弱点克服大学生の確率・統計」：

 

弱点克服大学生の確率・統計

弱点克服大学生の確率・統計

 

 前回↓

 

ryosuke-okubo.hatenablog.com

 

 

問題

問題69 統計量Ⅱより改変

x_1,x_2,...,x_nが正規分布N(\mu,\sigma^2)から独立に発生したデータであるとき，平均\muと分散\sigma^2の最尤推定量を求めよ。

 

解法

まず尤度関数について定義づける。

パラメータ\thetaのときに値Xである確率は，

P(X|\theta)

と表せる。一方，尤度関数は値Xが観測されたときのパラメータ\thetaの尤度，

L(\theta|X)

と表される。確率を確率密度関数に拡張して，一般に

L(\theta|x) = f(x|\theta)

かなりたつ（注意：尤度は確率ではない）。

f:id:ryosuke_okubo:20190428103758p:plain
f:id:ryosuke_okubo:20190428103804p:plain

 

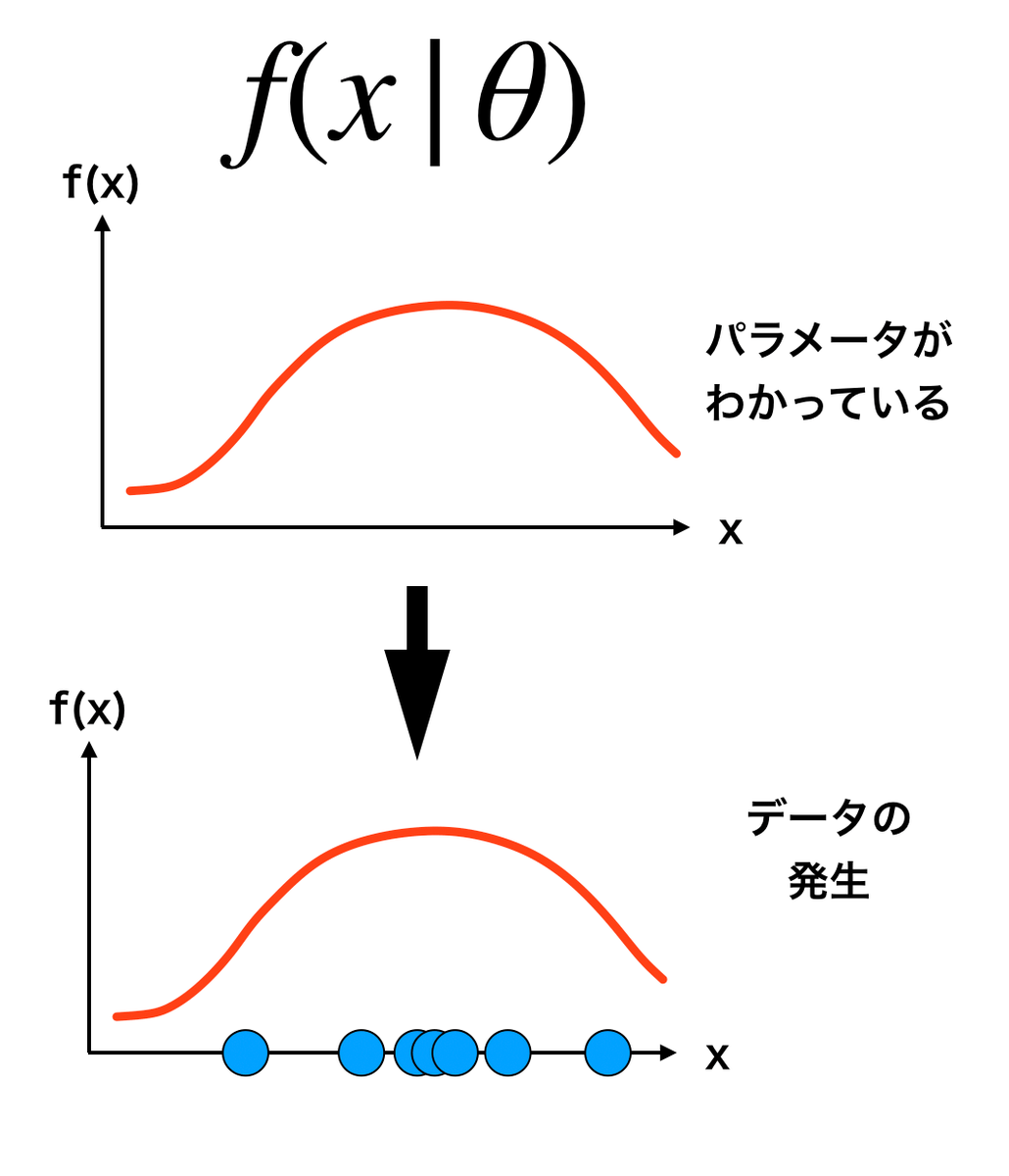
データが複数ある場合，尤度関数は

L(\theta|x_1,x_2,...,x_n) = f(x_1,x_2,...,x_n|\theta) \\ {\displaystyle = p(x_1)p(x_2)...p(x_n) = \prod_{i=1}^N p_i }

となる。

よって正規分布の尤度関数は

{\displaystyle L(\mu,\sigma^2) = \prod_{i=1}^N \frac{1}{\sqrt {2 \pi} \sigma} e^{-\frac{(x_i - \mu)^2}{2 \sigma^2}} = (\frac{1}{\sqrt {2 \pi} \sigma})^N e^{-\sum_{i=1}^N \frac{(x_i - \mu)^2}{2 \sigma^2}}}

と表せる。ここで

{\displaystyle \prod_{i=1}^N x_i = x_1 \times x_2 \times ... x_n }

である（総乗）。

 

最尤推定とは，尤度関数L(\theta|x)（以後xを省略）が最大になるパラメータ\thetaを求めることである。最大化するにおいて，対数尤度関数

{\displaystyle \ln{L(\theta)} = \ln{\prod p(x_i)} = \sum \ln{p(x_i)}}

で計算すると楽である。ここで最尤推定量\hat{\theta}は

{\displaystyle  \frac{\partial}{\partial \theta}\ln{L(\theta)} = 0}

となる\thetaである。

よって正規分布では

対数尤度関数：{\displaystyle \ln{L(\mu,\sigma^2)} = \frac{1}{2 \sigma^2} \sum(x_i - \mu) + \frac{N}{2} \ln{2 \pi \sigma^2}}

それぞれ偏微分して0と置くと，

{\displaystyle  \frac{\partial}{\partial \mu}\ln{L(\mu,\sigma^2)} = -\frac{1}{\sigma^2}\sum(x_i - \mu)= 0}

 {\displaystyle  \frac{\partial}{\partial \sigma^2}\ln{L(\mu,\sigma^2)} = -\frac{1}{2 \sigma^4}\sum(x_i - \mu)^2 + \frac{N}{2\sigma^2}= 0}

これらの式を連立させて解いたものをそれぞれ\hat{\mu}，\hat{\sigma^2}と置くと，

{\displaystyle \hat{\mu} = \frac{1}{N}\sum x_i}

{\displaystyle \hat{\sigma^2} = \frac{1}{N}\sum (x_i - \hat{\mu})^2}

となる。

 

応用として，回帰分析における最尤推定が重要である。y_i = ax_i + b +\epsilon_iの誤差\epsilon_iについて

と仮定したときの最尤推定量は，最小二乗法における正規方程式の解と一致する。

 

クラメール・ラオの不等式に到るまで

最尤推定の延長として， 

  • スコア関数
  • フィッシャー情報量
  • クラメール・ラオの不等式

について簡単に説明する。

 

スコア関数

定義：

{\displaystyle S(x;\theta) = \frac{\partial}{\partial \theta} \ln{L(\theta|X)}}

つまり，対数尤度関数の微分である。なお，期待値は0である。

{\displaystyle E [ S(x;\theta)|\theta ] = 0}

 

フィッシャー情報量

定義：

{\displaystyle I(\theta) = E [ S(x;\theta)^2|\theta ] }

スコア関数の2次モーメントで定義される。 スコア関数の期待値が0であることから，分散と同義である。

{\displaystyle I(\theta) = V [ S(x;\theta)|\theta ] }

 

クラメール・ラオの不等式

定義：

{\displaystyle V(\hat{\theta}) \ge \frac{1}{I(\theta)}}

簡単にいうと，予想される分散はフィッシャー情報量の逆数以上である。

 

まとめ

ここまで全12回を4ヶ月に渡って投稿してきた。実際に問題を解くことで，数理統計学にある式の意味がわかるようになったように思う。扱った内容はいずれも基礎的な話であり，今後の応用にどう結びつけるかが重要であろう。

 

（終）